APPLICATION OF SCHRODINGER WAVE EQUATION

Application of Schrodinger Wave Equation

Particle in a One Dimensional Deep Potential Well

Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.

The potential function is expressed as

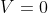
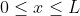
$V=0$ for $0\leq x\leq L$ ……..(1.60)
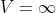
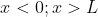
$V=\infty$ for $x<0;x>L$ ……..(1.61)

Figure 1.9 : Particle in deep potential well

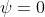
The probability of finding the particle outside the well is zero (i.e. $\psi =0$ ). Inside the well, the Schrödinger wave equation is written as

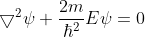
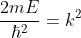
$\bigtriangledown ^{2}\psi +\frac{2m}{\hbar^{2}}E\psi =0$ ……..(1.62) Substituting $\frac{2mE}{\hbar^{2}}=k^{2}$ ……..(1.63), and writing the SWE for 1-D
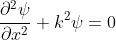
We get $\frac{\partial^2 \psi }{\partial x^2} +k^{2}\psi =0$ ……..(1.64)
The general equation of above equation may be expressed as
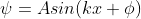
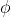
$\psi =Asin(kx+\phi )$ ……..(1.65) Where A and $\phi$ are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation (1.65)
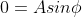
$0=Asin\phi$
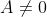
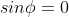
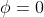
As $A\neq 0$ then $sin\phi =0$ or $\phi =0$ ……..(1.66)
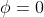
Condition II: Further ψ = 0 at x = L, and $\phi =0$ ,therefore from equation (1.65)
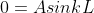
$0=AsinkL$
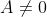
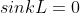
As $A\neq 0$ then $sinkL=0$ or $kL=n\pi$

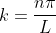
$k=\frac{n\pi }{L}$ ;n = 1,2,3,4,…. ……..(1.67)

Substituting the value of k from (1.67) to (1.63)
$\left (\frac{n\pi }{L} \right )^{2}=\frac{2mE}{\hbar^{2}}$
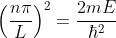
This gives $E=E_{n}(say)$

$\boldsymbol{E_{n}=\frac{n^{2}\pi ^{2}\hbar^{2}}{2mL^{2}}}$ n = 1,2,3,4,…. ……..(1.68)
From equation (1.68) E_n is the energy value (Eigen Value) of the particle in a well. It is clear that the energy values of the particle in well are discrete not continuous.

Figure 1.10 : Energy for Particle
Using (1.66) and (1.67) equation (1.65) becomes, the corresponding wave functions will be
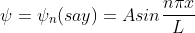
$\psi =\psi _{n}(say)=Asin\frac{n\pi x}{L}$ ……..(1.69) The probability density $\left |\psi \right |^{2} =\psi \psi^{*}$
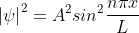
$\left |\psi \right |^{2} =A^{2}sin^{2}\frac{n\pi x}{L}$ ……..(1.70)

The probability density is zero at x = 0 and x = L. since the particle is always within the well $\int_{0}^{L}\left |\psi \right |^{2}dx =1$

$\int_{0}^{L}A^{2}sin^{2}\frac{n\pi x}{L}dx=1$
$A^{2}\int_{0}^{L}sin^{2}\frac{n\pi x}{L}dx=1$
$A^{2}\frac{L}{2}=1$
$A=\sqrt{\frac{2}{L}}$
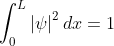
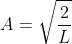
Substituting A in equation (1.68), we get
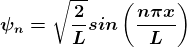
$\boldsymbol{\psi _{n}=\sqrt{\frac{2}{L}}sin\left ( \frac{n \pi x}{L} \right )}$ ; n = 1,2,3,4,…. … (1.71) The above equation (1.71) is normalized wave function (Eigen function) belonging to energy value E_n

Figure 1.11 : Wave function for Particle

A free Particle

A particle is said to be free when no external force is acting on during its motion in the given region of space, and its potential energy V is constant.

Let us consider an electro is freely moving in space in positive x direction and not acted by any force, there potential will be zero. The Schrodinger wave equation reduces to

$\bigtriangledown ^{2}\psi +\frac{2m}{\hbar^{2}}E\psi =0$ …(1)Substituting, we get
$\frac{2mE}{\hbar^{2}}=k^{2}$

As the electron is moving in one direction (say x axis), then the above equation can be written as

$\frac{\partial^2 \psi }{\partial x^2}+k^{2}\psi =0$ ….(2)The general solution of the equation (2) is of the form $\psi =\psi _{o}e^{-i\omega t}$

The electron is not bounded and hence there are no restrictions on k. This implies that all the values of energy are allowed. The allowed energy values form a continuum and are given by

$E=\frac{\hbar^{2}k^{2}}{2m}$ ….(3)

The wave vector k describes the wave properties of the electron. It is seen from the relation that $E\alpha k^{2}$ . Thus the plot of E as a function of k gives a parabola.

The momentum is well defined and in this case given by

$p_{x}\psi =\frac{h}{i}\frac{\partial \psi }{\partial x}$

Therefore, according to uncertainty principle it is difficult to assign a position to the electron.

physicsgurus

Sunday, September 9, 2018

APPLICATION OF SCHRODINGER WAVE EQUATION